Ένας ιστορικός τρόπος για να προσεγγίσουμε την έννοια των πρώτων αριθμών είναι η εξέταση της χρήσης των κλασμάτων με διαφορετικές βάσεις. Μέσω των αιγυπτιακών κλασμάτων που λειτουργούν με τη βάση 10 και των ακκαδιακών κλασμάτων που λειτουργούν με τη βάση 60, μπορούμε να ερευνήσουμε τα μονοπάτια της λήθης. Ενώ τα αιγυπτιακά είναι ιερογλυφικά και τα ακκαδιακά μερικώς συλλαβικά και μερικώς ιδεογραφικά, τα κλάσματά τους αντιμετωπίζουν τις ίδιες δυσκολίες ως προς τον υπολογισμό τους όταν δεν διαιρούν τη βάση.

Βέβαια, στα αιγυπτιακά υπάρχουν περισσότεροι βαθμοί ελευθερίας διότι η επιλογή των κλασμάτων του αθροίσματος δεν είναι καθορισμένη. Η βάση 10 δεν ορίζει τη σειρά των πράξεων. Ενώ με τη βάση 60, στη Μεσοποταμία υπήρξε μια συστηματοποίηση των υπολογισμών. Η διαφορά προέρχεται και από τα διακριτικά στοιχεία που επέτρεπαν στους Αιγύπτιους να έχουν ειδικούς ιερογλύφους για όλες τις δυνάμεις του 2 έως το 64 για τα κλάσματα του τύπου 1/n. Επιπλέον, δεν είχαν προβλήματα με τα κλάσματα αυτού του τύπου. Μέσω της μονάδας (|), της δεκάδας (∩) και της εκατοντάδας (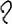), μπορούσαν να γράψουν το κλάσμα 1/987 με τον εξής τρόπο:

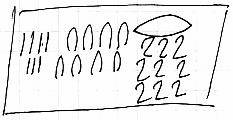
Το μοναδικό τους πρόβλημα προερχόταν από τα κλάσματα του τύπου α/b, τα οποία έπρεπε να μετατρέψουν με τον ακόλουθο τρόπο. Π.χ. 47/60 γράφεται ως 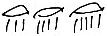δηλαδή 1/3+1/4+1/5. Μέσα σε αυτό το πλαίσιο υπήρχαν κλάσματα που ήταν πολύ πιο δύσκολα για τους Αιγύπτιους ως προς την ανάλυσή τους. Αυτά τα κλάσματα είχαν ως παρονομαστή έναν αριθμό που δεν διαιρεί τη βάση, δηλαδή το δέκα. Την ανάλογη δυσκολία βρίσκουμε και στα ακκαδιακά. Δεν υπάρχει δυσκολία στη γραφή εφόσον: VVV< < < < VVVVV σημαίνει 3,45 ή μέσω της βάσης 60: 3*60 + 45*1 = 180 + 45 = 225 Ενώ με τα κλάσματα έχουμε: 1/2 = 0;30 1/3 = 0;20 1/4 = 0;15 1/5 = 0;12 1/6 = 0;10. Όμως το κλάσμα 1/8 αναγκάζει ήδη τη χρήση της δεύτερης βάσης εφόσον έχουμε: 0;7,30. Η πραγματική δυσκολία εμφανίζεται με το κλάσμα 1/7. Και στην ουσία, βλέπουμε ότι αυτοί οι μη κανονικοί αριθμοί για αυτά τα συστήματα δεν έκρυβαν μόνο τα ελαττώματα των συστημάτων αλλά και τις ενδογενείς ιδιότητες των πρώτων αριθμών.