Abstract
To study the odd prime values of the Ramanujan tau function, which form a thin set of large primes, we compute Lehmer-Ramanujan Probable Primes.

Keywords Ramanujan function · Primality · Lucas sequences

Definition 1
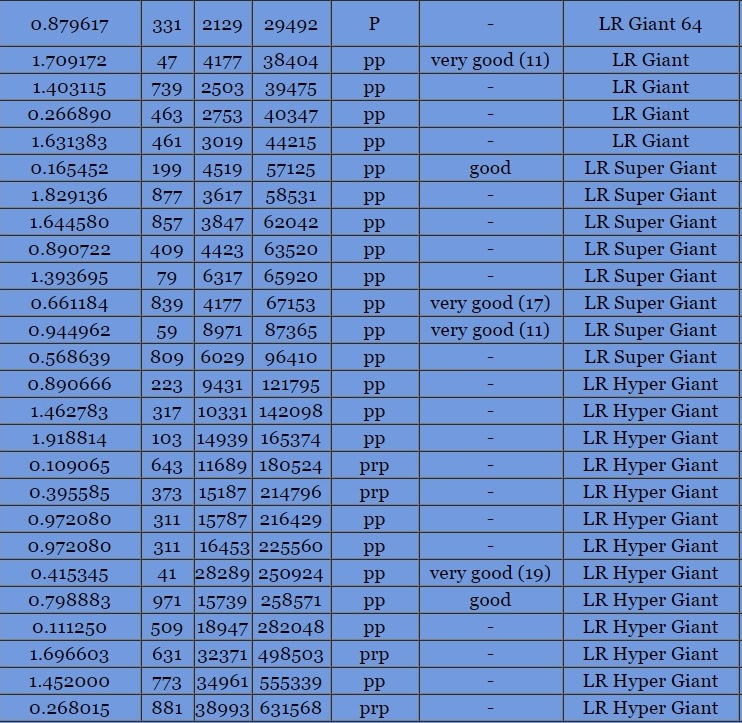
Let p,q be odd primes. Then we define LR(p,q) := τ(p^(q−1)).
More generally, we shall use the notation LR(p,n) := τ(p⁽ⁿ⁻¹⁾) for all positive integers n and we set the value LR(p, 0) := 0.

Theorem 1
Let n be a positive integer such that τ(n) is an odd prime.
Then n = p^(q−1) where p and q are odd primes and p is ordinary.

Theorem 2
Let p and q be two odd primes, p ordinary.
If d is a prime divisor of LR(p,q), then d ≡ ±1 (mod 2q) or d = q.
Moreover, q|LR(p,q) if and only if q|Dp.

Theorem 3 Let p be an ordinary odd prime. I
f p ≡ 1 (mod 4), then LR(p,p) is composite.
If p ≡ 3 (mod 4) and d is a prime divisor of LR(p,p), then d ≡ ±1 (mod 4p).

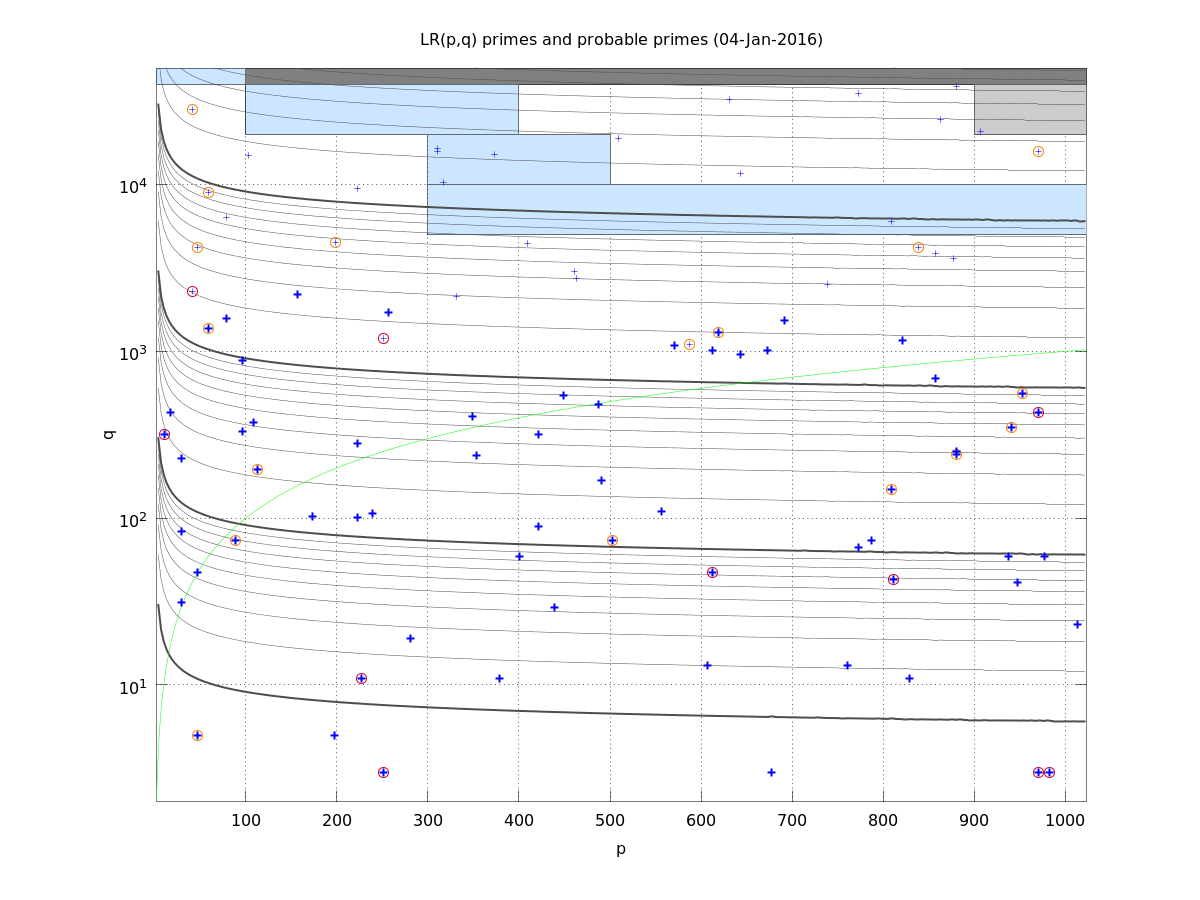
LR probable primes

Reference: N. Lygeros, O. Rozier : Odd prime values of the Ramanujan tau function. The Ramanujan Journal Vol. 30, March 2013