6005 - La théorie des marchés en tant qu’extension de la théorie des jeux III. (avec P. Gazzano)
P. Gazzano, N. Lygeros
Les contrats échangés sur les marchés financiers apportent des exemples simples de jeux à deux joueurs, qu’ils soient à somme nulle ou non nulle. Les contrats futures et les options vanilles sont respectivement des jeux à deux joueurs à somme nulle et non-nulle.
Un contrat future conclu en date 0 est un accord entre deux parties d’échanger à une date T un actif à un prix K fixé en 0. Un agent sait qu’il devra acheter un actif à une date ultérieure T et qui anticipe une hausse du cours va vouloir se couvrir contre la hausse et va prendre une position longue sur un contrat future. La contrepartie qui aura vendu un contrat vendra donc l’actif en T. Contrairement à l’acheteur qui se couvre contre une hausse des cours, le vendeur du contrat anticipe une baisse des cours et se couvre contre cette baisse.
Lorsque le contrat arrive à son terme, l’acheteur achète au vendeur du contrat la quantité d’actif définie dans les clauses du contrat au prix K. Pour déterminer les gains et les pertes, nous comparons le prix du contrat par rapport au prix réel en T de l’actif. Cela nous donne donc une estimation des gains ou des pertes. Les gains ou les pertes en T seront donc égales à ST – K, ou K est le prix fixé à l’avance.
Si ST≥K alors l’acheteur est gagnant sur le contrat, et le vendeur perd K – ST. En effet, l’acheteur achète l’actif au prix K. Mais ce prix étant inférieur au prix ST qu’il aurait obtenu sur le marché, il est gagnant de ST – K, et le vendeur est perdant de la même quantité.
Si ST≤K alors l’acheteur est perdant sur le contrat, et le vendeur gagne ST – K. En effet, l’acheteur achète l’actif au prix K. Mais ce prix est supérieur au prix ST qu’il aurait obtenu sur le marché, il est donc perdant de K – ST, et le vendeur est gagnant de la même quantité.
Un tel contrat est donc un jeu à somme nulle, puisque le gain gagné par l’acheteur est totalement compensé par la perte par le vendeur du contrat – et réciproquement – si les anticipations se réalisent.
Nous pouvons alors formaliser dans le cadre de la théorie des jeux un contrat future comme ceci :
- le nombre des joueurs est 2, le joueur 1 représente l’acheteur et le joueur 2 représente le vendeur.
- les stratégies sont : les niveaux d’achats pour l’acheteur (entre 1 et 10) et les niveaux de ventes pour le vendeur (entre 1 et 10).
- les payoff sont égaux à H(Si,Sj)=Si – Sj, 0≤j≤N, 0≤i≤N.
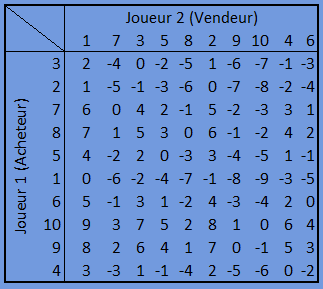
Nous obtenons alors la matrice suivante :
Max(Min(H(Si,Sj)))=Max(Min(H(Si,Sj)))=0
Cet exemple illustre la présence de points selles prévus par la théorie de Von Neumann dans le cas de jeux à somme nulle à deux joueurs avec une information parfaite.
Dans le cas des options – call ou put – contrairement aux futures où les parties ont l’obligation d’honorer leurs contrats, les acheteurs ont le choix d’exercer ou non l’option qu’ils détiennent. Une option est le droit d’acheter ou de vendre un actif à une date donnée à un prix fixé à l’avance. Considérons une option d’achat sur un actif dont le prix est C.
Supposons qu’un agent désire acheter en T un actif financier, et pense que le cours de cet actif peut monter. Il peut alors décider d’acheter un call, qui lui donne le droit (et non l’obligation) d’acheter l’actif en T au prix K fixé à l’avance.
- Si le prix de l’action augmente et dépasse K, il exerce son call et le gain est ST – K – C. Il achète ainsi un actif à un prix plus bas que le prix du marché et est dans ce cas gagnant.
- Si le prix de l’action diminue et devient inférieur à K, alors l’acheteur n’exerce pas le call et le gain est -C, mais que l’on peut assimiler à 0.
Les gains seront donc Max(ST – K,0) et l’acheteur du call sera assuré d’avoir un gain non négatif.
La contrepartie amenée à vendre ce call sait qu’elle va devoir vendre en T. Si elle anticipe une baisse du prix de l’action, alors elle peut se couvrir en vendant un call à un prix K.
- Si le prix de l’action diminue et devient inférieur à K, l’option n’est pas exercée, et le vendeur gagne C, le prix que l’acheteur a versé pour acheter ses options.
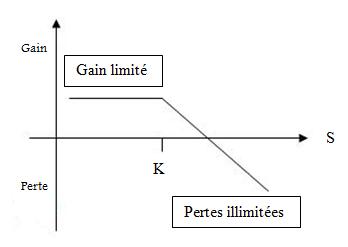
- Si le prix de l’action augmente et dépasse K, alors le call est exercé et le vendeur devra vendre à un prix plus bas que le marché. La perte sera donc égale à K + C – ST.
Nous voyons ainsi dans ce cas que le jeu n’est plus à somme nulle. La condition du contrat lorsque K≤ST fait qu’il n’est pas à somme nulle puisque les flux versés dans ce cas ne s’annulent pas. Ainsi, le risque est supporté par le vendeur du call. Nous avons donc le graphique suivant :