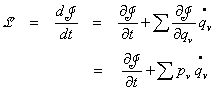2781 - Καταγραφή της επιστολής του Α. Einstein στον Κ. Καραθεοδωρη (06/09/1916) Transcription de la lettre d’A. Einstein à C. Carathéodory (06/09/1916)
N. Lygeros
|
6. IX. 16. Lieber Herr Kollege ! Sie haben mir in Aussicht gestellt, mir Wir setzen nun Hieraus erhält man beide Jakobische Gleichungs-
|
|
|
Zweitens ist als Anfangsbedingung gegeben, also Bahn konstant sind. Fröhot man statt der Durch Differenzieren von (2) nach der Zeit
|
|
|
Damit ist natürlich noch keineswegs die |

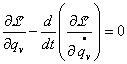 …..(1a)
…..(1a) … (3)
… (3)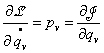 ….(3a)
….(3a)