Η μάθηση των αριθμών ταυτίζεται στην κλασική εκπαίδευση με τη μάθηση των σχημάτων των αριθμών. Αυτή η ταύτιση έχει ένα ενδογενές πρόβλημα. Ξεχνά την αφαιρετικότητα του σχήματος των αραβικών αριθμών. Αυτοί οι αριθμοί δεν έχουν ένα αυτονόητο σχήμα. Το σχήμα τους είναι αποτέλεσμα μίας γεωμετρικής εξέλιξης.
Συνεπώς, το σύστημα των αριθμών δεν πρέπει να βασίζεται σε αυτά τα σχήματα όταν έχουμε την πρώτη επαφή με τις αριθμητικές έννοιες σε μικρή ηλικία όταν το παιδί δυσκολεύεται να σχηματίσει τους αραβικούς αριθμούς. Διότι ακόμα και η αντιγραφή αποτελεί μία δυσκολία.

Στο επόμενο παράδειγμα βλέπουμε πώς ένα παιδί 4 ετών αντιμετωπίζει την αντιγραφή των αραβικών αριθμών. Η έλλειψη κατανόησης της δομής αυτών των αριθμών είναι προφανής. Ακόμα και η αναγνώριση των αριθμών είναι μία δυσκολία.

Στη συνέχεια βλέπουμε την καταγραφή του ρωμαϊκού συστήματος. Η αντιγραφή έχει νόημα αυτήν τη φορά τουλάχιστον στους αριθμούς που είναι συμμετρικοί. Όμως αντιλαμβανόμαστε και ένα άλλο στοιχείο. Το παιδί σχηματίζει το συμμετρικό και όχι το σχήμα του αριθμού.

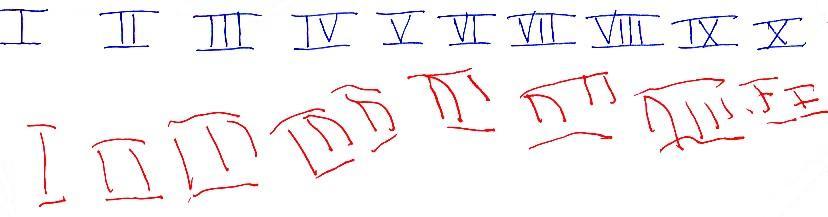
Η δεύτερη προσπάθεια της αντιγραφής ενισχύει την τάση της πρώτης. Η γραμμικότητα επιτρέπει μία καλύτερη αντιγραφή. Και η συμμετρία φαίνεται ακόμα πιο ξεκάθαρα.

Το ρωμαϊκό σύστημα μπορεί να χρησιμοποιηθεί σε πρώτη φάση διότι η προσθετική ιδιότητά του και η γραμμικότητα επιτρέπουν ευκολότερη επινόηση της αντιστοιχίας μεταξύ σχήματος και αριθμού. Επιπλέον, η προσθετική ιδιότητα δεν εμφανίζεται μόνο ως αφαιρετικό σύστημα. Λειτουργεί και ως δομικό πλαίσιο που διευκολύνει την αντιγραφή των αριθμών.

Γενικότερα, θα λέγαμε ότι η μάθηση των αριθμών θα έπρεπε πρώτα να περάσει από απλούστερα συστήματα όσον αφορά στη γραμμικότητα της δομής. Αυτό σημαίνει ότι ο δάσκαλος θα πρέπει να ξέρει και άλλα συστήματα εκτός από το αραβικό, για να έχει ένα μεγαλύτερο φάσμα, έτσι ώστε να εξετάσει πιο αποτελεσματικά την ανταπόκριση του παιδιού. Το ευρύ φάσμα επιτρέπει και περισσότερη δημιουργικότητα. Με αυτόν τον τρόπο, η προσέγγιση των αριθμών μπορεί να είναι και βιωματική και νοητική.

Το νοητικό σχήμα που ακολουθεί αυτή η προσέγγιση είναι βιολογικό. Το παιδί στην εμβρυακή του ανάπτυξη περνά από στάδια που ανήκουν στην εξέλιξη της αλυσίδας στην οποία ανήκει ο άνθρωπος. Στη μάθηση του παιδιού, η εξέλιξη της γραφής των αριθμών δίνει ιδέες στον τομέα της διδακτικής και αναδεικνύει την αξία της ιστορίας των μαθηματικών για τη μάθηση των αριθμητικών συστημάτων.