Ayache, Sharif et Vu Dinh Hoa ont établi une nouvelle formule sur les arbres, de manière élégante et élémentaire. Cette formule permet de relier de manière universelle le cardinal de l’arbre, le degré du sommet considéré avec la distance de ce sommet à tout autre de l’arbre. La démonstration s’effectue par récurrence sur la distance maximale associée à un sommet. Ainsi ils ont obtenu :

où V est l’ensemble des sommets de l’arbre
où d(q) est le degré du sommet q
et où l(v,q) est la distance entre les sommets v et q.

De plus en introduisant la notion de transmission d’un graphe selon la terminologie de Plesnik c’est-à-dire :
(transmission d’un sommet)

(transmission du graphe)

ainsi que l’indice de Wiener à savoir :

où la somme est prise sur tous les couples {u, v},
il est facile de voir que . Il est alors possible de définir la distance moyenne de G comme

où p est l’ordre de G, selon la terminologie de Gutman.

De cette manière, les auteurs prouvent que si un arbre T est d’ordre p>1 alors directement à partir de la formule initiale. Une conséquence

indirecte de ce résultat est la formule suivante. Celle-ci aussi est obtenue par un calcul direct.

Si dans un arbre T d’ordre p>0 et de degré maximal d>2, tout sommet est de degré 1 ou d alors :

.

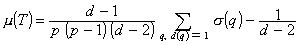Cela permet de constater que dans ce type d’arbres, comme le signalent les auteurs de la formule, la distance moyenne ne dépend en réalité que des sommets de degré 1 i.e. des feuilles de l’arbre.

Cependant la performance calculatoire la plus remarquable des auteurs, c’est l’établissement d’une formule explicite de la distance moyenne d’un arbre planté de hauteur h (h>2) qui a une racine et dont le degré de tout sommet interne est d (d>2) et où à chaque niveau i, il y a sommets. Le calcul explicite s’effectue en quatre étapes pour aboutir au final à :

.

La maîtrise de ces calculs emboîtés permet de constater d’une part la puissance de la première formule obtenue par Ayache, Sharif et Vu Dinh Hoa et d’autre part que grâce à l’emploi d’une stratégie calculatoire adaptée il est possible d’obtenir des résultats explicites même dans le cadre d’une distance moyenne dans les arbres. Grâce à cette approche, nous pouvons supposer l’existence de résultats à venir dans ce domaine.