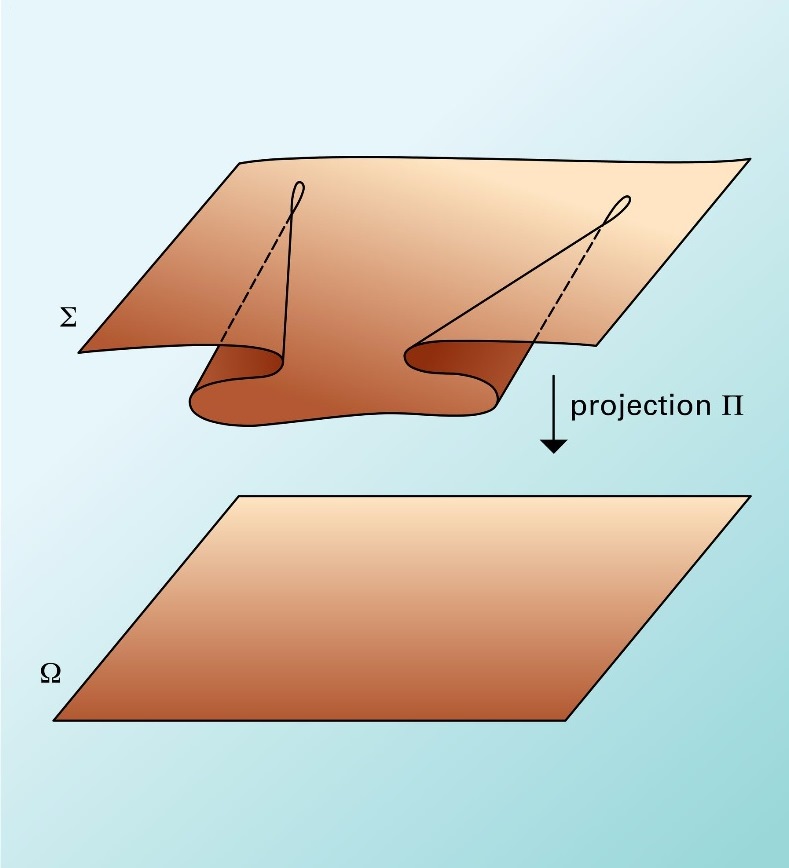
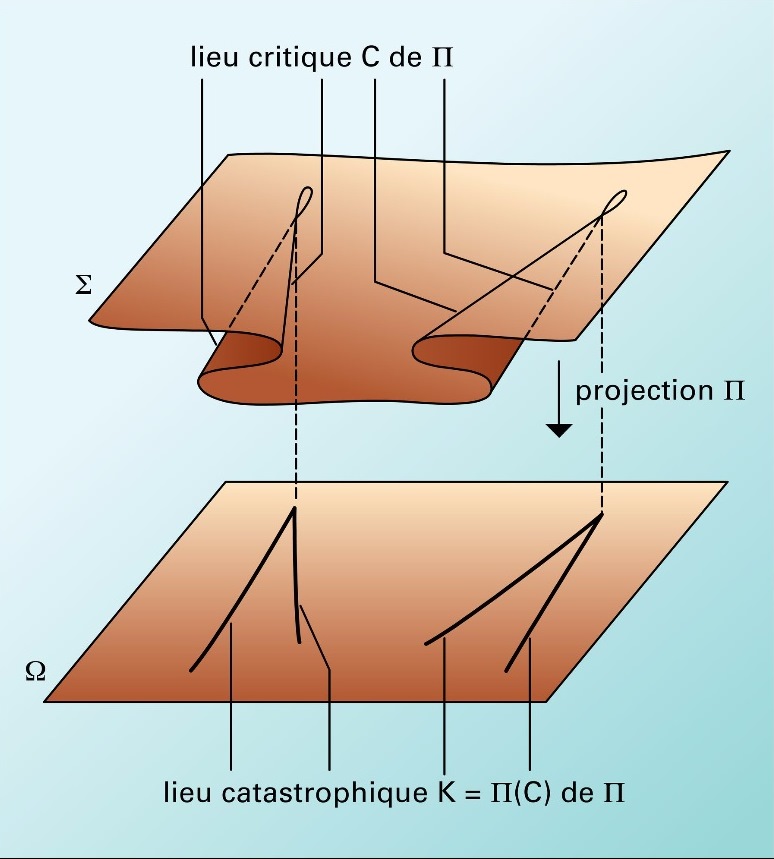
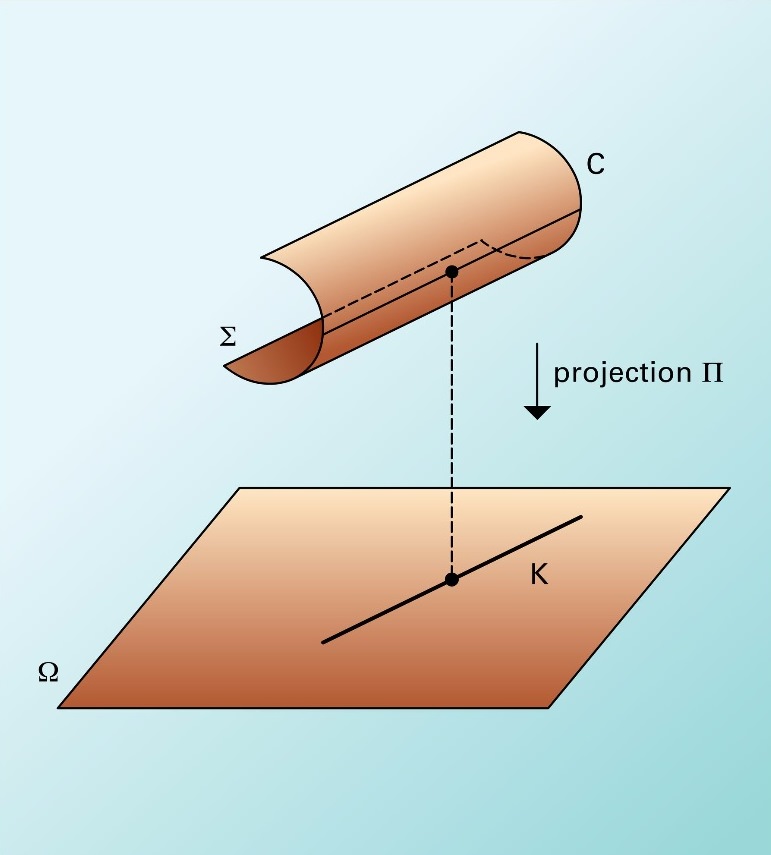
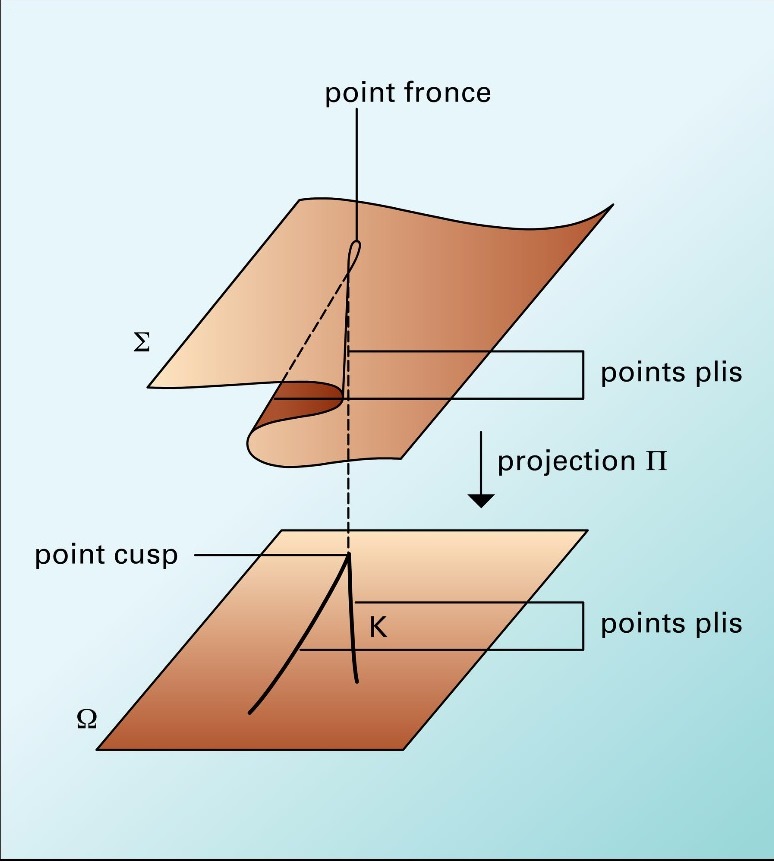
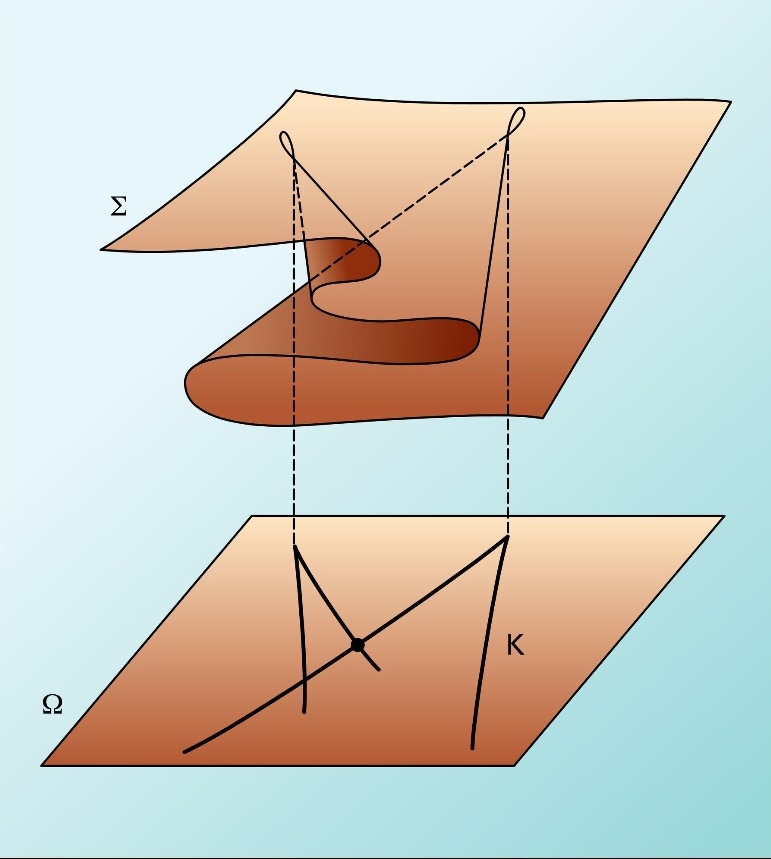
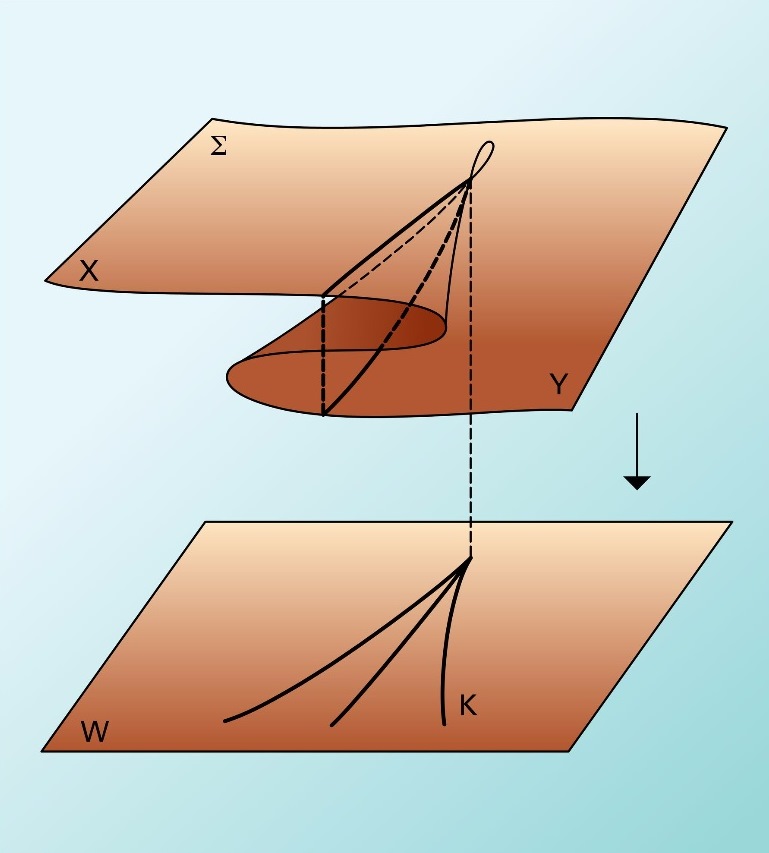
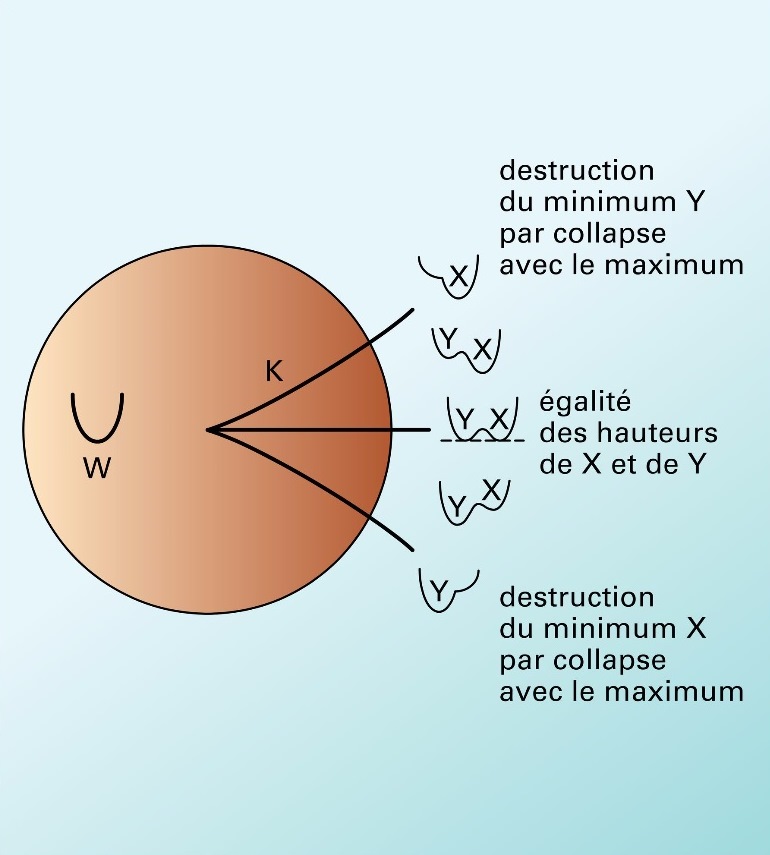
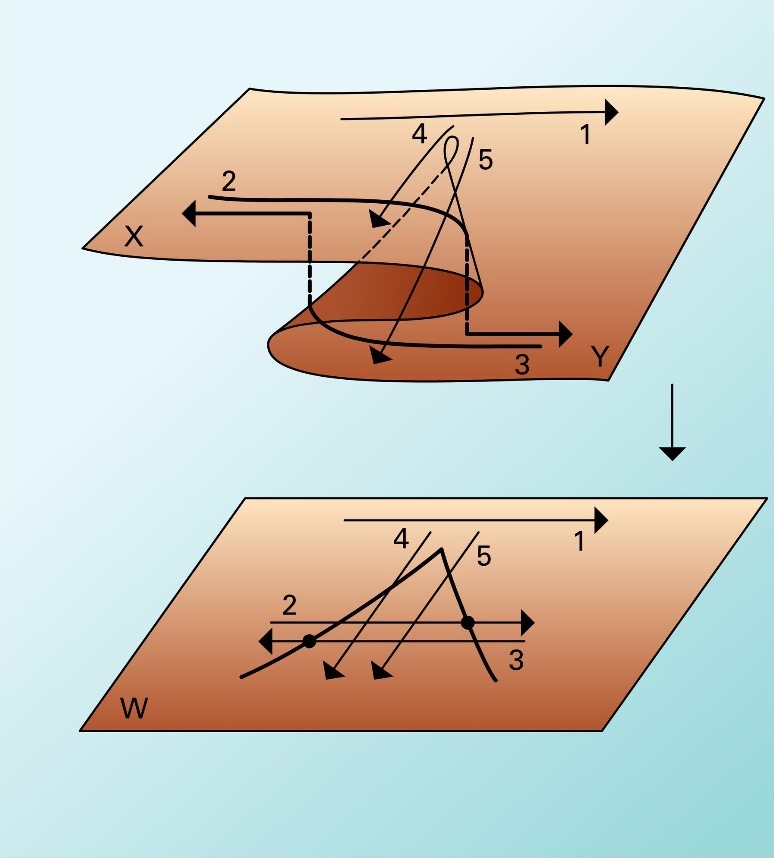
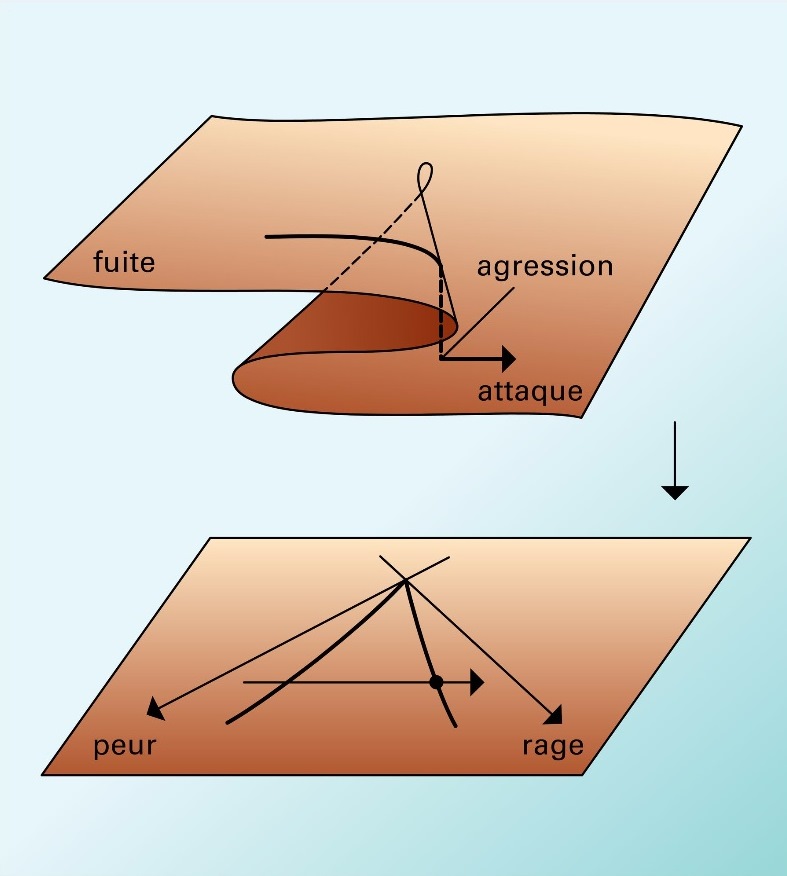
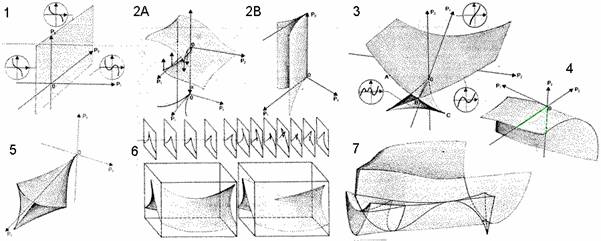
With the catastrophe theory, R. Thom managed to classify the catastrophes according to the number of input parameters, the number of unknown output parameters, and price of the system dynamics.
For a and x we have: x³+ax

For (a, b) and x we have: V = x⁴+ax²+bx
For (a, b, c) and x we have: V = x⁵+ax³+bx²+cx
For (a, b, c) and (x, y) we have: V = x³+y³+axy+bx+cy
or x³/3-xy²+a(x²+y²)+bc+y
For (a, b, c, d) and x have: V = x⁶+ax⁴+bx³+cx²+dx
For (a, b, c, d) and (x, y) we have: V = x²y+y⁴+ax²+by²+cx+dy
With these data we can also utilize the ADE classification by Arnold, through the simple Lie groups .
This practically means, that someone who knows these mental schemes, will function differently during a negotiation, and will take advantage of catastrophes, taking in to account the input parameters, in order to predict continuity, even when there are phenomena of discontinuity.
In practical terms, someone who does not comprehend the subject, as many plans as he may have, he will achieve a balance, only if the other factor want’s him to do so, otherwise he is situated at the dead end of the branchings.