144 - An Introduction to Dendrominos (with J. Scoville)
N. Lygeros, J. Scoville
This article deals with a special class of polyominos – the undivided polyominos of minimal area. More intuitively, these polyominos form unbranched chains with distinct ends. The area, A, and perimeter, P, of such a polyomino are related by P=2(A+1). Since the dual of a polyomino in a square lattice is a tree, we shall call these constructions dendrominos. The boundaries of a dendromino are the cells whose maxima in the dual tree are of degree one. A dendromino of n>1 cells has exactly two boundary cells. Examples of dendrominos follow:
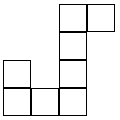
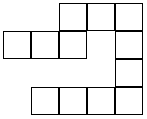
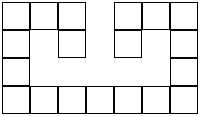
Figure 1: Dendrominos
The rightmost dendromino is a member of a special class of dendromino. Since no cells may be added to produce a larger dendromino, we say that it is a terminal dendromino. A minimal terminal dendromino is a terminal dendromino with a minimal number of cells. The rightmost dendromino above is a two dimensional minimal terminal dendromino, consisting of 19 cells. In three dimensions, the minimal terminal dendromino has 23 cells:
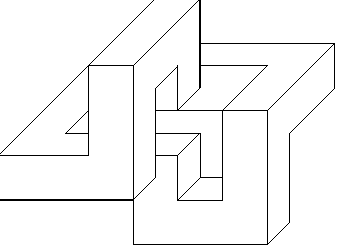
Figure 2: The 3-d minimal terminal dendromino has 23 cells.
Since the n-cube tiles n-space, the concept of a cubic dendromino extends naturally to higher dimensions. In general, the minimal terminal dendromino in n dimensions has 8n-1 cells. A minimal arrangement is produced when cells are placed at positions +/- 1 on the x-axis and at +/- 2 on every axis. These cells are then connected by minimal paths to form a dendromino. The z-w cross-sections of the 4-d minimal terminal dendromino follow:
| x=-2 | x=-1 | x=0 | x=1 | x=2 | |
| y=2 | ….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
..X.. ..X.. ..XXX ….. ….. |
….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
| y=1 | ….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
..X.. ….. ….X ….. ….. |
….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
| y=0 | ….. ….. XXX.. ….. ….. |
….. ….. X.X.. ….. ….. |
XXX.. X…. X…X ….. ..X.. |
….. ….. ..X.. ….. ..X.. |
….. ….. ..X.. ..X.. ..X.. |
| y=-1 | ….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
….. ….. ….X ….. ..X.. |
….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
| y=-2 | ….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
….. ….. ….X ….X ..XXX |
….. ….. ….. ….. ….. |
….. ….. ….. ….. ….. |
Figure 3: A 4-d minimal terminal dendromino has 31 cells.
Terminal dendrominos with k cells exist for all k>18 in two dimensions. These may be constructed by adding cells in multiples of two to the 19- and 20-celled dendrominos. In three dimensions, terminal dendrominos exist for all k>29. It is unknown whether even terminal dendrominos exist in three dimensions for k<30.
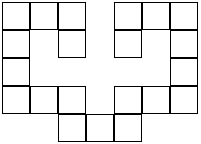
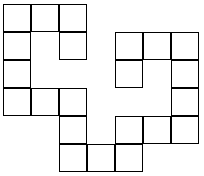
21-celled dendromino 22-celled dendromino
Dendrominos are not, in lower dimensions, restricted to a cubic lattice. In two dimensions, for example, dendrominos can also exist in triangular and hexagonal lattices. The minimal terminal dendromino in a hexagonal lattice has 13 cells, and the minimal terminal dendromino in a triangular lattice has 20 cells.
The maximal filling of an n-cube of side length k (where k is odd) with a dendromino is 2((k+1)/2)^n-1 cells. In two dimensions, it is possible to obtain a maximal filling with a terminal dendromino.
Special thanks are extended to Jim Ferry for mathematical contributions and to Jennifer Kasten for translation services.
References:
N. Madras, C.E. Soteros, S.G. Whittington, J.L. Martin, M.F. Sykes, S. Flesia and D.S. Gaunt : The free energy of a collapsing branched polymer. Journal of Physics A: Mathematical and General, 23, p.5327-5350. 1990.
S. Flesia, D.S. Gaunt, C.E. Soteros, S.G. Whittington : Statistics of collapsing lattice animals. Journal of Physics A: Mathematical and General, 27, p.5831-5846. 1994
R. Stanley : Enumerative Combinatorics. Cambridge University Press 1997.
